Over the past couple of weeks, I’ve been writing a small lexer in Rust, motivated by the need for something simpler and easier to use than the default lexer offered by LALRPOP. The in-built lexer allows for simple regexes, but managing these regexes becomes difficult for more sophisticated situations such as double-quoted literals.
The core idea behind a lexer is to convert a stream of characters into a stream of tokens. Each token constitutes a distinct building block that can be used to construct a grammar for a language parser. As an analogy, the vocabulary and punctuation supporting the English language constitute a set of tokens. Of course, you could avoid the lexer altogether and deal directly with the underlying characters, but that makes the language grammar exponentially more complex to specify. Imagine parsing English sentences based on rules associated with each character of the alphabet!
How It Works
To recap, a lexer’s job is to convert a stream of characters into a stream of tokens. Tokens can be anything that’s useful to feed into your parser. The parser is generated from a set of productions declared in a grammar file. LALRPOP provides a bottom-up LR(1)1“LR(1)” expands to a left-to-right, rightmost derivation parser with a single token lookahead. parser. A bottom-up parser uses recognized tokens to construct leaf nodes of the parse tree. In contrast, a top-down parser (of which recursive-descent parsers are the most common) generates productions eagerly as matching symbols are encountered. Top-down parsers are often very convenient and easy to use, but they’re less flexible compared to bottom-up parsers, and require backtracking when they encounter production dead-ends.
One way to structure the lexer is to break it down into a number of processors, one per type of token that you could potentially produce. For example, a Sym processor processes symbols, which are arbitrarily long consecutive sequences of characters conforming to a class (such as letters, numbers and underscores). The processor abstraction is useful for encapsulating logic associated with each token type into its own implementation. The idea is to iterate through each character in the stream, and feed it to each of the processors until one of them accepts the character. If none of the others accept the character, the Err processor is sure to do so (which means the character stream is ill-formed).
This abstraction is represented by the following trait:
pub trait Processor {
fn accept(
&self,
idx: usize,
chr: Option<&char>) -> Result<LexRes, LexErr>;
}To complete this definition, the associated types LexRes and LexErr are provided below. The lexer — when fully or partially successful — returns an ordered set of tokens, where each token declares the starting index of the token (relative to the original character stream), the length of the stream consumed, and the type of token (represented by the Cat enum). Notice that some of these enum values such as Sym (for ‘symbol’) and Lit (for ‘literal’) capture a value, whereas others do not.
#[derive(Debug, Eq, PartialEq)]
pub struct LexRes {
pub tokens: Vec<Token>,
pub accepted: usize,
pub rejected: bool,
}
#[derive(Debug, Eq, PartialEq)]
pub struct LexErr {
pub idx: usize,
pub msg: String,
}
#[derive(Debug, Eq, PartialEq)]
pub struct Token {
pub idx: usize,
pub len: usize,
pub cat: Cat,
}
#[derive(Clone, Debug, Eq, PartialEq)]
pub enum Cat {
Sym(String),
Lit(String),
Assgn,
Eql,
SemiColn,
LParen,
RParen,
Spc,
}What the simple definition of LexRes above belies is its underlying flexibility. When a processor receives a character, it can choose from 3 options:
- Accept k outstanding characters (
accepted = k; k ≤ n) - Reject all characters not accepted (
rejected = true; k < n) - Wait for more characters (
rejected = false; k < n)
The number n represents the total number of outstanding characters, which increments on every iteration, but decrements on acceptance or rejection of characters. Notice that these options are not mutually exclusive; in fact, the first option combines with either the second or third, but the latter cannot be combined with each other.
When the processor chooses the third option, this acts as a signal to the lexer that the next character should be fed directly to this processor. In essence, the processor holds an exclusive lock over the remainder of the stream as long as characters remain pending (neither accepted nor rejected). This process can continue ad infinitum, or at least until the end of the character stream. In each iteration, the processor has the choice of accepting up to the total number of outstanding characters (in stream order), and either rejecting the rest (which ends the cycle and releases the exclusive lock) or continuing to wait for additional characters.
The declared ordering of processors has functional significance in certain situations. For instance, if you have a choice of detecting one of <, - and <- as different token types, you’d likely want the latter to have precedence. Also, as a trivial example, the Err processor is always used as the last resort.
Play the short animation below, for a concrete visual of what the lexer’s processing looks like for the simple character sequence:
let quote <- say("\"Hello world!\" --RRI");
In the example above, let, quote and say are interpreted as symbols using the Sym processor. The Seq processor looks for a specific sequence of characters (here, it is <-, mapping to Cat::Assgn). The Lit processor is distinctive because it internally tracks state associated with the escape character \, which can escape double-quotation marks inside a double-quoted literal.
Complexity
If we assume that (a) we have a small constant number of processors and (b) each processor performs its task in constant time, the overall algorithm is clearly O(n) in time-complexity, with respect to a character stream of length n. However, we can also evaluate how efficient the algorithm is with respect to a baseline. In theory, the only way for us to be certain that a character is part of a particular token is for its processor to accept it, which means that every character must be processed at least once, giving us a total of n processing calls as the ideal minimum to baseline our algorithm against.
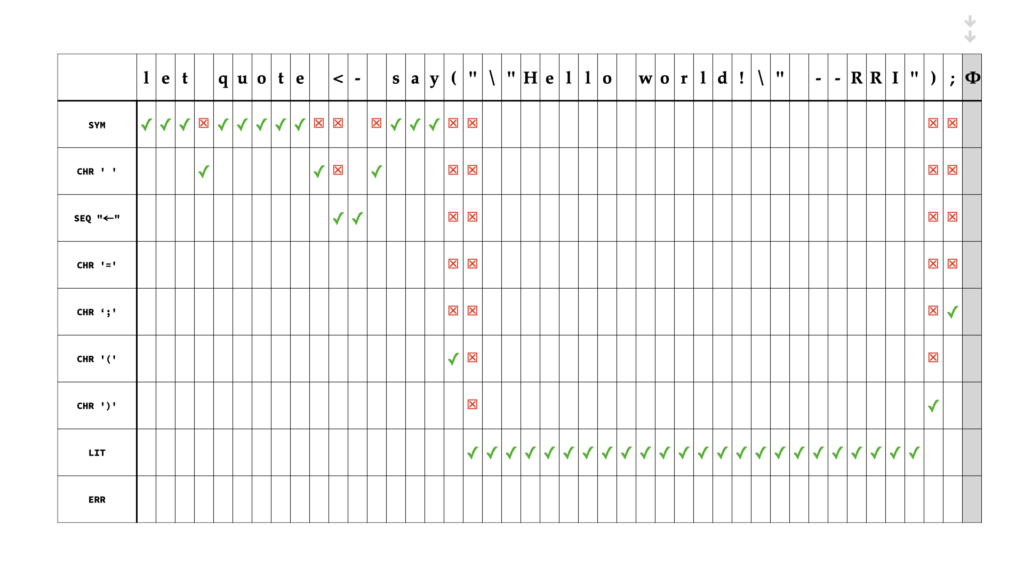
From the visual above, it’s clear that the checkmarks (✓) represent the ideal path, whereas the crosses (☒) represent ‘misses’, or distance traveled before the character is accepted. Further, when a processor like Sym rejects the character immediately succeeding its final character (such as whitespace or punctuation, which is not part of the symbol), processing is restarted at the rejected character from the first processor, which, in the particular example, is again Sym. That means we have an extra character to be processed for every symbol recognized (note that ‘symbol’ in this context means the output token of the Sym processor such as let, quote and say). The efficiency of the algorithm with respect to the baseline can therefore be defined as:
\frac{count(\texttt{accept})}{count(\texttt{accept}) + count(\texttt{reject}) + count(\texttt{symbol})}In essence, this is a number in (0, 1] that is the inverse of the average number of steps until a character is accepted by a processor. It varies based on the string processed by the lexer, so we’d likely only care about average statistics. Applying it to the example above gives us an efficiency of approximately 0.59: on average it takes 1.7 steps for each character to be accepted by a processor. Turning this into a useful metric would require us to normalize it, which we won’t attempt to do today.
Finally, there are further opportunities for refinement. First, each processor requires a different number of character comparisons to complete its task. Although we’ve assumed that each operates in constant time, we really ought to weight each processor, or otherwise measure the total number of comparisons directly. This would give us a more accurate metric than the one presented above. Second, we can order processors to maximize efficiency, basing the order on predictions that we derive from the statistics of the input being processed. We’re still bound by the need to process each character at least once, but we might be able to get really good at predicting which processor to try next, giving us an efficiency of close to 1.
That’s all for today, folks! 🖖
